In the Hough Transform,
the votes are distributed around the point of the true parameters (u0,v0)like a butterfly shape as shown by the meshes in Figure 2.
The estimated values of the parameters
are expected to be the quantized values of
the true parameter
(u0, v0).
Let
![]() and
and
![]() denote
the errors of the parameters.
denote
the errors of the parameters.
Since u is the scanning parameter,
we will be able to find the value of u whose error is
within the quantization error,
![]() ,
the absolute value of the error of the parameter v,
cannot be made smaller only by decreasing the sampling interval
,
the absolute value of the error of the parameter v,
cannot be made smaller only by decreasing the sampling interval ![]() .
The coordinates
.
The coordinates
![]() ,
which are substituted for
the transformation function, include the error of at most
,
which are substituted for
the transformation function, include the error of at most
![]() which comes from the quantization of image.
The parameter
which comes from the quantization of image.
The parameter ![]() also includes the error of at most
also includes the error of at most
![]() .
In general, vik is affected by these errors through the
transformation function.
Let
.
In general, vik is affected by these errors through the
transformation function.
Let
![]() be the difference (of the error) between vik
and the true parameter v0.
In order to make
be the difference (of the error) between vik
and the true parameter v0.
In order to make
![]() smaller in the Hough Transform,
smaller in the Hough Transform,
![]() must be made smaller.
We mainly discuss this non-quantized error in this document.
must be made smaller.
We mainly discuss this non-quantized error in this document.
The error of vi is given by
| = | |||
| = | |||
| (7) |
Note that the error measured along v-axis is affected
not only by the quantization of the image
but also by the quantization of the scanning parameter
in the Hough Transform.
This property is essential in the Hough Transform,
however, it has often been overlooked.
(8) denotes the errors
for only a single sampling point
(xi, yi).
If we consider all the sampling points on the line,
or if we consider the moving of a point along the line,
the errors
![]() are distributed
around v=v0 in the parameter space.
Each of the quantization errors and the transformation errors also
has a sort of distribution according to the change of i.
Regarding the distributions as probability distributions,
we can took at the errors as the noises which come from the probability distributions.
Let NQ and NT denote these noises,
and we call them
``quantization noise'' and ``transformation noise'' respectively.
A real distribution of votes at
are distributed
around v=v0 in the parameter space.
Each of the quantization errors and the transformation errors also
has a sort of distribution according to the change of i.
Regarding the distributions as probability distributions,
we can took at the errors as the noises which come from the probability distributions.
Let NQ and NT denote these noises,
and we call them
``quantization noise'' and ``transformation noise'' respectively.
A real distribution of votes at
![]() (the quantized value of u0)
is expected to be the same distribution as a random variable vT, where
(the quantized value of u0)
is expected to be the same distribution as a random variable vT, where
| (9) |
When we design a system which requires the Hough Transform,
we may often try to make the maximum value of errors smaller,
or to make the average value of errors smaller.
Here, we give the definition of the maximum absolute values of
the quantization errors and
those of the transformation errors when (xi,yi) takes various values.
A ``maximum quantization error,'' which is denoted by
qv or qv(u0), is defined as the maximum absolute value of
the quantization errors
![]() .
From (8) and
.
From (8) and
![]() ,
we get
,
we get
The distribution of the quantization noise NQ follows that of the
quantization error ![]() ,
because
the transformation function
Fv is a linear function of y.
It is known that
,
because
the transformation function
Fv is a linear function of y.
It is known that
![]() follows a discrete distribution
for the sampling of images with square grid
if the tangent of the angle between x-axis and a straight line is a
rational number.
It is also known that
follows a discrete distribution
for the sampling of images with square grid
if the tangent of the angle between x-axis and a straight line is a
rational number.
It is also known that ![]() follows a continuous, uniform distribution
for a infinitely long line
if the tangent is an irrational number.
We can regard the distribution of the quantization noise NQas a continuous and uniform distribution Qin the range
[-qv, qv] as shown in
Figure 3.
follows a continuous, uniform distribution
for a infinitely long line
if the tangent is an irrational number.
We can regard the distribution of the quantization noise NQas a continuous and uniform distribution Qin the range
[-qv, qv] as shown in
Figure 3.
In general,
![]() in the transformation error
in the transformation error
![]() is the linear function of the coordinates
x and y.
Therefore,
is the linear function of the coordinates
x and y.
Therefore,
![]() on a certain line is distributed uniformly from its minimum to
its maximum value.
We can easily verify
by the computer simulation
that the real transformation errors
on a certain line is distributed uniformly from its minimum to
its maximum value.
We can easily verify
by the computer simulation
that the real transformation errors
![]() have a uniform distribution.
have a uniform distribution.
We introduce some notations here.
| Rv0 | 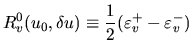 |
(13) | |
| = | 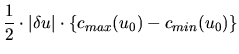 |
(14) | |
| voff | 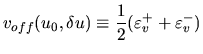 |
(15) |
Since ![]() is an unknown value,
and since the maximum value of Rv0 is important in the following discussion,
we use
is an unknown value,
and since the maximum value of Rv0 is important in the following discussion,
we use
![]() which maximize Rv0.
The maximum value is given by
which maximize Rv0.
The maximum value is given by
The distribution of vT is known to have a trapezoid shape. The upper base length of the trapezoid is 2|qv-Rv|, and the center of the upper base is v0+voff(Figure 3).
As the origin of the coordinate system gets apart from
the center of the image, the absolute value of the offset voff gets greater.
This means that the error of the estimated parameter for vincreases. To design precise Hough Transform, we should put
the origin on the center of the image.